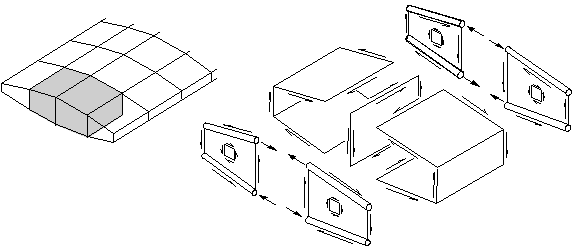
Figure 1: An assembly of panels and stringers is used to model part of an aeroplane wing [Adapted from Argyris 1960, Fig. 44].
The computational power of desktop computers increases every year which brings the advanced analysis software of research institutes closer to the designer in engineering practice. Nonlinear analysis programs are already being used to check completed designs and currently the first attempts are made to use them in the design process itself [for example Wittek 1998]. A nonlinear analysis takes much time and requires a specially trained engineer. Nevertheless, application looks promising because nonlinear models can be used to design less conservative and more reliable structures than is common nowadays.
The purpose of the research, presented in this dissertation, is to investigate the application of nonlinear models in design processes. Our efforts are focused on reinforced concrete walls and deep beams because of two practical problems with these structures that require a nonlinear model to be solved. First, it is commonly believed that walls and deep beams are substantially over-reinforced if redistribution of forces is not taken into account. Second, many engineers feel that crack widths cannot be determined accurately in plasticity based models.
Thus, we set out to develop a computer program for design of reinforced concrete walls that includes nonlinear material behaviour. To be successful the program had to meet four criteria: It has to be simple, reliable, accurate and fast. As can be expected it turned out difficult to satisfy all these requirements perfectly. Therefore we aimed at a balanced compromise based on the behaviour of reinforced concrete, the design process and its purpose.
In the subsequent sections of this chapter some history and the relations with parallel research are presented. In Chapter 2 the stringer-panel model is introduced as a simple approximation of wall behaviour and its application in a design process is discussed. In Chapter 3, stringer-panel results are compared to experiments in order to test the accuracy of the model. Chapter 4 gives an example of a successful design procedure. Finally, Chapter 5 gives the conclusions of the research. Most of the derivations and theory are presented in the appendices in order to keep the main text comprehensible.
When Joseph Monier patented his large reinforced concrete flowerpots in 1867, it was unclear how to design with the new material. Contractors, like François Hennebique in France, made ever larger structures based on experience and full scale experiments. Just before the turn of the century, reinforced concrete was developing fast. For example the firm "AG für Monierbauten" constructed 200 reinforced concrete bridges in Germany in the short period from 1890 until 1897 [Leonhardt 1964, p. 41].1
Gradually the theory for modelling the structural elements was developed. For beams the concrete in the compression zone was assumed to be a linear-elastic material though it was understood that this was a conservative approximation [Mörsch 1908, p. 83]. The truss model for shear design of beams was formulated by Wilhelm Ritter in 1899 and improved by Emil Mörsch in 1902 based on experimental observations. Many researchers have suggested different stress distributions in the compression zone of a beam. A comprehensive historical overview can be found in the dissertation of Eivind Hognestad [Hognestad 1951] who became well known in North America for including normal forces in the beam theory. Currently, in the American ACI code the rectangular stress block is adopted which is attributed to C.S. Whitney [Whitney 1937]. In the Eurocode the parabolic-rectangular stress strain diagram is used which can be traced back to O. Baumann [Baumann 1934]. Many researchers have refined and expanded the truss model to make it more accurate and applicable to interactions of shear, torsion and bending. Due to the importance of beams and columns in structures the discussion on how to model them best is still continuing.
Though concrete is not a convincing plastic material, plasticity theory has shown to be very successful to explain experimental observations of reinforced concrete. It was given its foundation independently by A.A. Gvozdev in 1936 Russia and later by William Prager and others at Brown University [Nielsen 1984, p. ix] [Gvozdev 1960] [Prager 1951]. Both derived the upper and lower bound theorems which had already been known intuitively long before they discovered them [Witteveen 1976]. Limit analysis was not only used to explain the behaviour of laboratory specimens but whole structures as well. It was applied to structural concrete by Bruno Thürlimann and others from Switzerland who developed and promoted the method with stress fields closely related to the strut-and-tie method [Muttoni 1997].
In Denmark Knud Winstrup Johansen developed the yield line method for slabs in his 1943 dissertation using the upper bound of the plasticity theory [Johansen 1962]. Before him already in 1921 the yield line method was applied by Aage Ingerslev on several examples [Ingerslev 1923]. As a reaction to the unsafe nature of the yield line method Arne Hillerborg developed the strip method in Sweden using the lower bound of plasticity theory [Hillerborg 1974]. Continuing in the Danish tradition Mogens Peter Nielsen developed the stringer method for walls and many other plastic solutions to structural concrete problems [Nielsen 1984]. Only recently, the yield line method was implemented in promising design software used at the University of New South Wales in Australia [Singh 1997].
In 1979 Jörg Schlaich in Germany started to work on strut-and-tie models for structural discontinuities such as joints and corners to explain structural concrete behaviour to his students. Together with his co-worker Kurt Schäfer and many Ph.D. students he systematically organised and further developed the strut-and-tie concept [DAfStb 1994]. In 1987 the knowledge on strut-and-tie models was summarised in a landmark paper [Schlaich 1987]. Though not very accurate, the strut-and-tie method is generally considered as an improvement of the empirical design rules, especially in situations for which no experiments are available. (see also Section 1.5). A serious concern is still the choice of a correct strut-and-tie scheme in case of statically indeterminate structures.
The plasticity based methods have been used to design structures successfully, for example the Storebæalt bridge connecting islands of Denmark in 1990. However, building authorities fell back on the classic elasticity theory for calculating stress distributions. They were concerned about the durability of the structures and did not trust crack control in a design based on plasticity theory. Moreover, computer programs had been developed that could conveniently compute the elastic stresses in both small and large structures. Impressive offshore structures were designed using only elasticity theory like the Troll in 1990.
The development of nonlinear finite element models of reinforced concrete was accelerated at the IABSE conference of 1981 in Delft. At that occasion Michael Collins initiated a contest to predict the response of 4 reinforced concrete panels that were scheduled to be tested. The contributions from 27 teams clearly showed what was missing in the models of that time [Blaauwendraad 1982].2
Hajime Okamura and a team of researchers in Japan developed a finite element software for dynamically loaded shear walls with the name WCOMR [Okamura 1991]. Vladimir Cervenka in the Czech Republic developed a two dimensional finite element program for statically loaded reinforced concrete with the name SBETA [Cervenka 1992]. Since then many more finite element programs for reinforced concrete have been developed and are being developed.
Frank Vecchio in Toronto provided much of the data for the software with large scale panel tests and he developed a simple constitutive model for membrane forces [Vecchio 1986]. The recent scrutinising by Thomas Hsu at the University of Houston with independent panel tests confirms much of the developed constitutive models [Pang 1995].
A three dimensional model of reinforced concrete was developed in 1993 at the University of Toronto [Selby 1993]. The effect of structural size on the ductility is recognised and included in most models (localisation). Size effect on the structural strength is addressed in some papers but the researchers do not yet agree on a quantification [Bazant 1998] [Carpinteri 1998].
Next to the practice-oriented approach of Collins and Vecchio in Canada, in The Netherlands a fundamental approach was adopted by Jan van Mier and René de Borst. The research concentrates on more academic issues like softening of plain concrete, lattice models and higher-order continua [Mier 1997] [Weihe 1998].
To date, models of reinforced concrete are still being improved but they can predict behaviour of reinforced concrete reasonably well. A misprediction of about 10% of the maximum load is commonly accepted since the scatter in material properties is of the same order. It seems that the theory of structural concrete is fully developed and only maintenance of the models is required due to changes in the material or its application. The challenges of today are introduction of the theory into practice and education.
In 1993, Blaauwendraad started to use the discrete element method to model reinforced concrete walls and deep beams with openings.3 After a preliminary study that resulted in the author's masters thesis, it was decided to continue the effort and develop a nonlinear design tool for reinforced concrete walls [Hoogenboom 1994].
Blaauwendraad wrote down his thoughts that had lead to the concept of the stringer-panel model in the "Festschrift" of the 60th birthday of J. Schneider [Blaauwendraad 1994]. The paper introduces the stringer-panel method as an intermediate of the strut-and-tie method and the linear finite element method. He writes that in practice, "... the resulting reinforcement consists of one or more concentrated tension bands situated near the edge and a distributed reinforcement over the plate or over large parts of it, often even applied in two orthogonal directions." A stringer-panel model adopts this reinforcement layout in advance and turns it into a discrete model of a structure. (See page 14 for a detailed description of the model.)
In the early days of the finite element method - when it was still referred to as the matrix method - a model similar to the stringer-panel model was used to calculate stresses in aeroplane wings and fuselages. Argyris and others developed the linear-elastic algorithms of computing stringer forces and panel stresses [Argyris 1960]. Around 1960 dominantly the force method was used in order to reduce the number of variables that had to be processed by the early computers. Much effort was put into developing procedures to automatically select the redundant variables. However, with the continuous increase of computer memory, the displacement method became applicable which appeared much easier to program and to use than the force method. The aircraft model, which is sometimes referred to as boom-panel system has been applied successfully by aircraft companies for many years. The model is still being used in teaching aerospace engineering.

Figure 1: An assembly of panels and stringers is used to model part of an aeroplane wing [Adapted from Argyris 1960, Fig. 44].
In Denmark, already in 1979 the stringer method was developed by Nielsen and others for reinforced concrete walls [Kærn 1979]. This method, which is very similar to the stringer-panel method, optimises reinforcement for a given load using the lower bound theorem of plasticity theory. Development of computational algorithms for optimisation recently renewed interest in this method at the Technical University of Denmark as is described in the next section. The stringer method has a long tradition in Denmark and is taught every year to students of structural concrete.
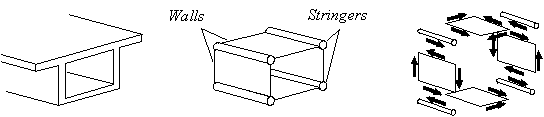
Figure 2: The Model Code advises to use a stringer-panel model to determine the distribution of forces in the walls of a box-girder [CEB-Bulletin 1993, Fig. 6.5.1 and 6.5.2].
Recently, the Model Code 1990 suggested a stringer-panel model in order to generalise models for specific cases [CEB-Bulletin 1993 pp. 187-188]. The Code refers to it as a stringer-and-wall model used for distributing section forces in thin-walled members or box-girders. The Code uses a plasticity approach since no comments are made on compatibility of the stringers and panels. It emphasises that the model is only valid in parts without discontinuities. The discontinuities can be treated separately with strut-and-tie models.4
In 1991, Connor of the Massachusetts Institute of Technology and others developed a model for shear lag in tall buildings [Connor 1991]. As yet the model is linear but work towards including nonlinear material behaviour is ongoing. A stringer-panel model was used to include all important parameters. Analytical relations are derived for a section of a tube. A simple computer program quickly computes the forces in a tube consisting of multiple sections.
At the Swiss Federal Institute of Technology (ETH) in Zürich, the team of Anderheggen works on a number of programs to optimise design of reinforcement. Their method starts to compute the linear-elastic stresses from which the designer can choose reinforcement fields. Subsequently, the program optimises the required reinforcement by allowing plastic deformations. Programs have been developed for walls and deep beams (DiBS), floors (PLATON) and folded plates (ORCHID). In 1996 the program PLATON was made available for practice as a Windows version and extended with filters for communication with other programs [Despot 1995] [Steffen 1996] [Tabatabai 1996].
As predecessors of this can be seen the work on optimisation of both strut-and-tie models and stress fields at the ETH supervised by Thürlimann [Schlaich 1989] [Hajdin 1990]. Currently at the ETH, the plastic design method is being validated with nonlinear finite element analysis (Glanzer).
At the University of Denmark related research is going on by two teams. The team of Damkilde concentrates on optimisation and plasticity theory applied to the stringer method [Damkilde 1993]. The team of Nielsen uses a discrete element approach including simple nonlinear material behaviour. The University will not develop graphical user-interfaces but they support an initiative of the company Ramboll to develop an interface for the stringer method [Jagd 1994].
At the University of Stuttgart in Germany, Schlaich and Schäfer supervised projects to develop graphical tools for strut-and-tie models. The team made many programs for different types of analysis around one data base. Programs are developed to identify stress trajectories, compute the ultimate load or optimise the shape of a strut-and-tie model by minimising its complementary energy. Some of the programs seem very promising but to the author's knowledge they have not been used outside the University [Rückert 1992] [Sunderman 1994].
At the same University a project was completed on the design of beams and walls with holes using strut-and-tie models [Hottmann 1995]. This project shows a striking absence of programming or even the use of computer tools.
At Purdue University (Indiana, USA), two researchers developed a program (NLSTAT) for interactive analysis of strut-and-tie models under supervision of Ramirez [Alshegeir 1992] [Yun 1996]. At this University and others in North America a substantial number of dissertations and papers have been devoted to strut-and-tie modelling of various structural elements like pile caps, brackets, post-tension anchor zones and deep beams.
The first days of structural concrete is recorded accurately in [Mörsch 1908, pp. 216-221].
A one page summary of the development of constitutive models for reinforced concrete in finite element programs can be found in the preface of the book of Okamura and Maekawa [Okamura 1991].
The discrete element method is often considered as predecessor of the finite element method [El Naschie 1990, pp. 221-237]. The structural material (stiffness and mass) and forces are lumped or swept into lines and points. To date it is still successfully used for dynamic computations and education with close relations to the more mathematical finite difference method. At Delft University much experience has been obtained in both software engineering and structural modelling from developing the discrete element program TILLY [Blaauwendraad 1994].
Recently the name discrete element method is also used for models of large numbers of particles [Williams 1993]. Not only the applications of this method are completely different from the method in this dissertation but also the computational algorithms to solve the ensuing set of nonlinear equations. It is the author's opinion that it is better to use the name distinct element method for particle models which is already being used by several authors in this field.