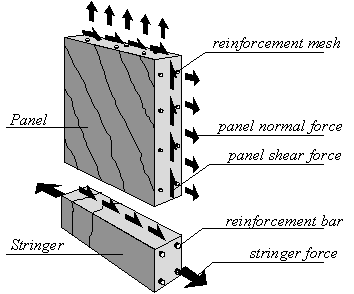
Figure 3: Stringers and panels are the building blocks of a concrete wall model.
The general development in structural engineering is towards full automatic design software that excludes human intervention. In this vision, the most an engineer has to do is start the program, tell it what it should do, wait a while and check the results. Two strategies are used in this pursuit; optimisation and expert systems. On the first subject much research is going on, though practical applications are still rare. The second subject of expert systems is less popular as a research theme. The few researchers that are working in this field are still in the phase of analysing what is really going on in the mind of a designer [for example Gero 1997].
As might be obvious from the text, we do not agree with either of these developments. The best approach for people and computers is to do what each is good at. People are flexible and creative, and computers are fast and reliable. So, people should design and computers should analyse and check [see also Schneider 1993]. In this chapter the design philosophy of the stringer-panel model and its graphical user-interface is explained.
Suppose we have a nonlinear analysis program which is very fast and robust. How would we use this program in a design process? We could proceed as follows: Roughly design the structure based on experience and rules of thumb. Subsequently, feed this information to the program and compute the structural response to the load to see for example whether it cracks severely or fails. If it does, simply strengthen the design at the weak locations and make another computation. With some experience we should get a good design in a few design cycles.1
There are two problems related to this approach. First, such a fast program is not available on a normal desktop computer because the computer capacity is not sufficient yet. Of course, this problem will solve itself if we wait a number of years due to the ever growing computation capacity, however, in the research project it was decided to speed up the computation by means of a simplified structural model. The model is referred to as stringer-panel model and is described in Section 2.2.
The second problem is that it is often not easy to see what causes a failure and how to improve the design. For example the program can show that a deep beam cracks heavily and fails prematurely but it is not clear if the vertical shear reinforcement or the horizontal bending reinforcement should be strengthened. Even if we can identify a cause of failure it is not clear how much extra reinforcement is necessary to prevent failure. We could just try something but this can result in a large number of successive improvements which makes designing a cumbersome undertaking. So, this second problem requires a successful design process, which is described in Section 2.5.

Figure 3: Stringers and panels are the building blocks of a concrete wall model.
As can be observed in every day practice, the reinforcement of walls and deep beams consists often of a mesh reinforcement at the surfaces and reinforcing bars along the edges and around holes. Starting from this geometry we developed a discrete element model in which some elements called stringers contain main reinforcing bundles and others called panels contain a distributed reinforcing mesh (see Figure 3).
A structure is modelled as an assembly of stringers and panels, which are in perfect equilibrium (see Figure 4). A stringer is loaded by a constant shear force along its length and a discrete force at both ends. A panel is loaded by constant shear forces and normal forces on the edges.
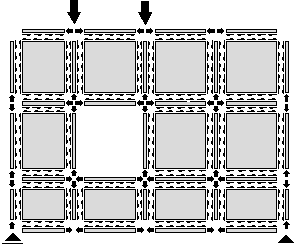
Figure 4: An exploded view of a stringer-panel model of a deep beam with a hole shows that all elements are perfectly in equilibrium. Note that normal forces at the panel edges are not present in this example.
The components of the model have grips that are connected by nodes. As Figure 5 shows, a panel has four grips with which it can be connected to adjacent stringers. A stringer has three grips with which it can be connected to other stringers, panels, supports or forces. (For more on nodes and grips see Footnote 6 on page 21).
Two versions of the model are developed; a linear version and a nonlinear version. In the linear version the material behaviour of the stringers and panels is linear-elastic and the panels carry only shear forces at the edges. No normal forces are carried by the panels because we want these forces to be transferred from the panels to the stringers in order to obtain the largest lever arm for the moment in a cross-section. This is in fact a local plastic redistribution included in the elastic model. Experience shows that this model results in the best initial design as explained in Section 2.5. The derivation of the stiffness matrix for the linear stringer is presented in Appendix 1. Similarly, the derivation for the linear panel can be found in Appendix 2.
Figure 5: A stringer-panel model can be assembled from simple components.
In the nonlinear version of the stringer-panel model, normal forces are included at the panel edges. This more accurate panel appeared necessary for two reasons. First, concrete dilates after the onset of cracking which influences the distribution of forces considerably. To include dilatation, a panel needs degrees of freedom perpendicular to the edges. Second, the distributed reinforcement contributes not only to the shear strength but also the normal strength of the material. An elegant way to include this strength is to add normal forces at panel edges.
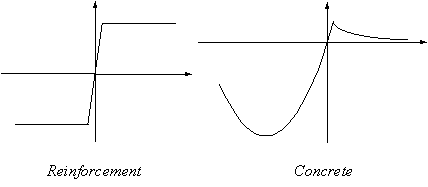
Figure 6: The accurate constitutive behaviour of the materials includes yielding and breaking of the steel and cracking and crushing of the concrete.
The stress field in a stringer is linear over its length. The derivation of the nonlinear stringer relations is presented in Appendix 1. The panel reference frame is derived in Appendix 4. The orthogonal x axis and y axis are as good as possible parallel with the panel edges. The panel normal stresses in the x and y direction are essentially linear in x and y, respectively. The panel shear stress field is linear in both x and y. Equilibrium is approximated in the panel and over the panel edges, nevertheless, the panel grip forces are in perfect equilibrium. The nonlinear panel relations are derived in Appendix 3. In the nonlinear model, the reinforced concrete material can both crack and crush and the reinforcement can yield and break as illustrated in Figure 6.
Engineering judgement is required to transform a real structure into a stringer-panel model: Stringers are drawn along edges, around holes, at supports and at concentrated loads. Panels are simply drawn in between the stringers. Less experienced designers may have to make a few improvements to get their first drawn model right. Compared to a strut-and-tie model a stringer-panel model is quite simple to make since you do not need to anticipate tension or compression nor to determine the inclination of struts. 2
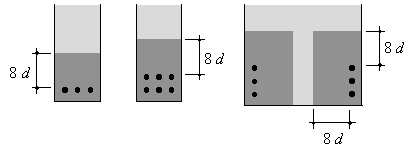
After a model is drawn and the elastic analysis is done the designer might want to improve the model for subsequent analysis (see Section 2.5 for more details on the design process). The position of a stringer in tension is easily decided because its centreline should represent the reinforcement: Simply put the stringer where you want to put reinforcement. The effective concrete area 3 depends on the number of reinforcing bars and the concrete cover as Figure 7 shows. The effective area reaches up to 8d from the bars, in which d is the bar diameter [Rückert 1992, p. 44]. It is important to use correct effective areas because this influences crack widths strongly.
A stringer in compression represents the compressed concrete in a part of the structure. Figure 8a shows a possible stress distribution at the edge of a concrete deep beam. At the left-hand side the concrete is crushing while at the right-hand side the concrete stresses are not as large. For a stringer to be in equilibrium with the part of concrete it represents, its centreline should connect the resulting forces. For the stringer to have the same deformation as the concrete, the stresses at its centreline must be the same as the stresses in the concrete. This determines the rectangular stress distributions (stress block) and the width of the stringer at each end (see Figure 8b). Though it is not difficult to derive a non-prismatic stringer, the very detailed information on how to draw this stringer is rarely available. Therefore, the stringer is approximated prismatically as shown in Figure 8c.
As can be seen in Figure 8b, the theoretical stringer dimensions can exceed the edge of the structure. If possible it is better to choose dimensions that remain inside the structures edges so that the computed distribution of forces is a statically admissible stress field. This will provide a safe strength according to the lower limit theorem of plasticity theory.
If in doubt about any dimension of the model it is advised to vary the parameter in question and evaluate the consequences. A change will often cause minor differences in the results. For example often the width of a compressed stringer hardly influences the deflections or the strength. Clearly, if a parameter does have a large influence it is better to choose a safe value. More details including examples on making stringer-panels models are presented in Chapter 4.
As explained above, a stringer-panel model consists of components that can be connected to model a structure. The association is easily made with children toys like wooden blocks or Legos. In the graphical program, the model should be just as simple to handle as a toy: Pick up a component, put it somewhere and connect it to other components. Fortunately, we did not have to invent this from scratch because a few good programs are already developed with many of these features. For example a simple drafting program like PowerPoint [PowerPoint] and a simulation program for mass-spring systems called Working Model [Working Model]. The name of the application we developed is SPanCAD which is derived from Stringer-Panel model for Computer Aided Design. 4
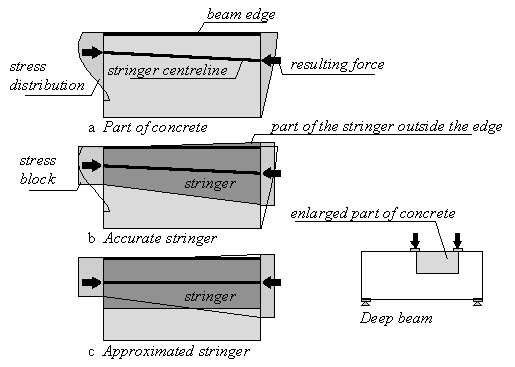
Figure 8: A stringer represents a part of concrete in compression at the edge of a deep beam.
When the development of SPanCAD began in 1994, the only appropriate programming platforms available were Visual Basic and AutoCAD. Visual Basic is an extended compiler with which an user-interface can be programmed by graphically selecting and positioning program components. A Visual Basic application has the advantage that it runs directly under Windows. However, it requires a skilful programmer to develop the drawing features needed.
On the other hand, AutoCAD is a popular program for computer aided drafting with many options for customising. An AutoCAD application is much easier to develop because much of the drawing tools are already present. In addition, data transfer between the different steps of the design process is easy in AutoCAD because architectural drawings are often made with AutoCAD and applications are available for drawing reinforcement. [for example AutoStruct 1997]. An important disadvantage is that the designer needs an expensive AutoCAD licence to be able to work with SPanCAD. 5
Figure 9: SPanCAD is an AutoCAD application for design of stringer-panel models. Click here for the full size figure
It was decided to develop SPanCAD as an AutoCAD application because we did not have the experience nor the time to develop an independent Windows application. To date, in 1998, more and better applications are available to build a graphical user-interface in Windows. However, for research, the author still prefers AutoCAD because of the speed in which a functioning tool can be created. Nevertheless, for successful use of stringer-panel models in practice, an independent Windows application should be built with the essential feature that it can communicate very well with other programs.
In SPanCAD, a stringer-panel model can be built out of a number of components. Figure 5 on page 16 shows that the components have grips which are used to change the position or shape of a component. If a grip of one component is positioned close to a grip of another, the program automatically connects the grips by a node. Conceptually, the nodes are devices to attach grips the same way bolts are used to connect steel plates. This is different from the traditional concept that a node is a point that defines the shape of an element. 6
Reinforcement of the components can be selected as bars or as cross-sectional areas. For example in a stringer, the designer can either select 3Ø16 bars or type 578 mm2 of reinforcement. It is advised to select bars because bar diameters are needed to compute crack widths. In addition, discrete bar sizes are usually a bit more than area reinforcement due to a round off, which often contributes to the strength of the structure. For example 3Ø16 has an cross-section of 603 mm2, which is 4 % more if only 578 mm2 is required.
The SPanCAD program is used next to other Windows programs like text editors, spread sheets and drafting programs (see Figure 9). Therefore, common Windows conventions such as mouse clicking and short cut keys are available. SPanCAD has a clear structure, on-line help and tutorials, which make it easy to learn.
It is not possible to separate the developed software from the theory. Much of the work presented was only possible because of the interaction between programming and using the program. Therefore, throughout the text, remarks are made about features of SPanCAD and their implementation in the computer code.
As pointed out in Section 2.1, it is not enough to have a simple nonlinear model and good graphical software in order to design a wall. Additionally, we need a successful design procedure, which is presented in this section.
To date in design practice, the reinforcement of walls is determined with either of two methods: the strut-and-tie method or a linear stress analysis with the finite element method. 7 The strut-and-tie method is based on the lower bound theorem of plasticity theory [Schlaich 1987]. The method is well developed, widely applicable and gives a good understanding of the structure at hand. Nevertheless, especially for walls it is not always clear which distribution of forces is the best and sometimes the ductility of reinforced concrete is not enough to allow the selected distribution to occur. Perhaps least practical, separate strut-and-tie models are often required for different load combinations.
Stress analysis of the structure with the finite element method using a linear-elastic material model is gaining popularity due to the availability of user friendly software. However, there is concern about the economy of the method. For example in case of slender beams, typically 25% more reinforcement is called for with a linear model compared to empirical methods or the truss analogy method [Roosen 1996].
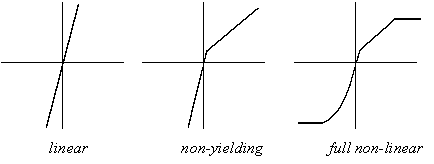
Figure 10: Several constitutive relations can be selected for the stringer behaviour. The linear behaviour is useful for initial design, the non-yielding behaviour is useful for improving the design and the nonlinear behaviour can be used when the design gets a final check.
Nonlinear finite element models are more accurate and do not have the previously mentioned problems. Currently they are only sometimes used to check completed designs because their computation time is considerable and a specialist is required to operate the software. Often improvements can be derived from the results but usually it is too late to change anything to the design. The challenging objective of the research presented in this text is to use nonlinear analysis in an early stage of the design process.
The design procedure we developed for structural concrete walls has the following steps (see Section 4.2 for more details):
In step 1 the structure is modelled with a stringer-panel model. Stringers are positioned on top of the drawing of the structure (see Section 2.3). Panels are drawn between the stringers. The dimensions of the stringers are estimated and the thickness of the panels are chosen equal to the wall thickness. Reinforcement quantities are not selected in this step of the design process.
In step 2 the load at the model is determined from the preliminary design of the whole structure. Safety factors are selected and subsequently, in step 3, the distributions of forces is computed by the software using a linear-elastic stringer-panel model. The envelopes of the stringer and panel forces are displayed conveniently.
In step 4 the stringer and panel forces are used to select reinforcing bars in the stringers and distributed reinforcement in the panels. The concrete dimensions of the stringers get appropriate dimensions.
In step 5 the distribution of forces is computed again but this time with a nonlinear model. This shows the influence of cracking of the concrete and yielding of the panel reinforcement on the distribution of forces. The software computes the behaviour of the nonlinear model for all load combinations individually. A special feature of this nonlinear computation is that the reinforcement of the stringers does not yield. Instead it continues to behave linearly beyond its yield strength (see Figure 10). Of course in the computation, proper design values of the material have to be used. (see Section 2.7).
In step 6 the results of the serviceability combinations are used to assess deformations and crack widths. The envelopes of stringer forces for all ultimate load combinations are used to select new stringer reinforcement if necessary. 9
In the simulation of step 7, the design gets a final check using full nonlinear behaviour of the material. Its ductility can now be assessed, which for example is important for earthquake loads.
Finally in step 8, the reinforcement is provided with anchorages and the stresses at the support platen are checked. More information on the design process including examples can be found in Chapter 4.
The most time-consuming part of designing is establishing the load on the structure. Therefore, an important task of any design program is to assist in managing loads.
Commonly, load is organised in load cases. For example heavy snowfall is a load case and a storm is one. 10 Load is not only limited to applied forces since also described displacements can be a load case for example to model a foundation settlement. 11 Also a temperature gradient can be a load case due to radiation of the sun. To emphasise the generality of the concept sometimes the name action or sollicitation is used instead of load. For computation, a load case is nothing but a set of tangible nodal forces and nodal displacements, conveniently organised in a vector.
It is a fact of live that if things go wrong, it usually is not because of one but of several reasons. For example, if a building collapses it is probably not only due to the storm but also because it had a large live load at the floors at that time. The building codes take this into account with load combinations. For example the code of the American Concrete Institute states [ACI 1995, art. 9.2.1 and 9.2.2] 12 :
0.9 U > 1.4 D + 1.7 L 0.9 U > 0.75 ( 1.4 D + 1.7 L + 1.7 W ) 0.9 U > 0.9 D + 1.3 W
In this, each line is a load combination which the structure has to withstand. The load cases are D, L, W, which stand for dead load, live load and wind load. The coefficients are safety factors. The left-hand side of the inequality is the strength U of the structure multiplied with a strength reduction factor. So simply stated, the strength should be larger than the combined loads.
Modern design software generates load combinations automatically according to a code of choice. Though this is not always the case, the software should allow a structural designer to edit the load combinations and add and remove ones. Every load combination represents a situation in which things can go wrong and the designer must use his experience and imagination to include all important combinations in his design. This interpretation is reflected in the name hazard scenario as sometimes used instead of load combination [Schneider 1994].
Codes of practice distinguish failures into ultimate and serviceability limit states. However, much more limit states are possible, like construction limit state, fatigue limit state and earthquake limit state. Simply stated a limit state is something that we do not want to happen to our structure. A set of load combinations is associated with each limit state. The safety factors of these combinations depend on the required reliability of the limit state. The required reliability depends on the consequences of failure and the costs to prevent it. 13 Some codes specify not only safety factors but reliability indices as well for different structure types and limit states. For example the Dutch code [NEN 1991, art. 5.3.4]. 14
A structure should not enter a limit state for each of the load combinations that are associated with that limit state. This is the main objective of the design process described in the previous Section 2.5. It includes computations of models of the structure with each load combination.
In SPanCAD the safety factors are organised in a matrix as Figure 11 shows. Standard load combinations are not generated since they are considered to be fundamental design knowledge and one of the few things the designer has to know in a computer supported design environment.
In a simulation of the structural behaviour the order in which the load cases are put onto the model can be very important. For example a structure will fail definitely if we first apply the self weight and subsequently the prestress. However, for most designs it is sufficient to increase the load cases proportionally until the full load combination is reached. In this respect it helps that the current formulation of the stringer-panel model is elastic, which makes it less sensitive to the order of loading than a model that incorporates accurate unloading behaviour. The load path can be chosen such that it includes all load combinations using the least computation time.
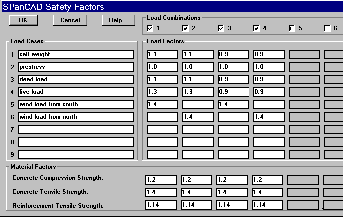
Figure 11: The table of safety factors in SPanCAD gives an overview of the load combinations of a limit state. Each row in the table is a load case and each column a load combination. Click here for the full size figure.
The number of load combinations that codes require to be checked for is increasing. Code makers correctly anticipate the use of software to deal with the laborious calculations. Moreover, in some large projects tailored safety factors are used so that less material can be applied [Kerstens 1996]. So, it can be expected that safety factors will become increasingly important in the future of structural design.
When a stringer-panel model is used to reproduce experiments on concrete walls - as in Chapter 3 - accurate material parameters have to be used. For example when a beam is tested the concrete and reinforcement properties are established with small tests. Subsequently, this data can be used in a simulation of the beam behaviour. However, when the stringer-panel model is used to design a structure the material parameters are not known accurately since the structure has not yet been constructed. So, safe values should be used for the material parameters.
It is not always clear what are safe values. For example it is obvious that we should use a low concrete compression strength but should we also use a low concrete stiffness? In this section it is explained that it is best to use average stiffnesses in order to describe redistributions accurately. 15
Figure 12 shows the results of tests on three concrete
cylinders which differ strongly due to the variability of the concrete
material. We assume that the tests represent the concrete properties at
three different locations in a wall. At a small load the stresses in the
wall will be small as shown in the figure with the blue dots  . When the load increases the stresses will increase too, as shown with
the green dots
. When the load increases the stresses will increase too, as shown with
the green dots  . This will continue until
at one location crushing starts, which is shown with red dots
. This will continue until
at one location crushing starts, which is shown with red dots  . Crushing is most likely to occur where the concrete strength is low and stresses are large.
. Crushing is most likely to occur where the concrete strength is low and stresses are large.
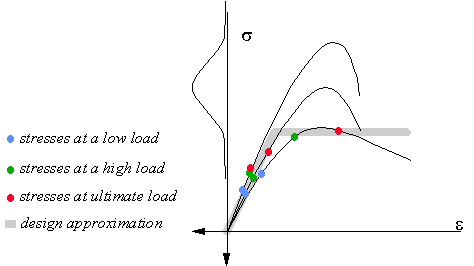
Figure 12: Stresses at three location of a concrete wall show that the bi-linear stress-strain diagram is a good approximation for design.
In a structural model for design we want to use only one stress-strain relation that represents the concrete at every location. The average bi-linear relation shown as a grey line in the figure represents the concrete well because it fits trough the dots. The bi-linear relation has the stiffness of the average quality concrete and the ultimate load and ductility of the low quality concrete.
Thus, when the stringer-panel model is used for the simulation of the behaviour of a design, safe values for the strengths have to be selected independent of the stiffness, ductility and other parameters of the material. Many reinforced concrete material models in literature do not fulfil this requirement because their parameters cannot be selected independently.
Additionally, the design could be optimised by removing material at locations where it does not seem to be necessary. For example in case of reinforced concrete we can remove reinforcement at locations with small cracks or low stresses.
Though the program is not made for it, SPanCAD can also be used to draw strut-and-tie models. Just use stringers and leave out the panels. For detailing, strut-and-tie models are considered more accurate and more comprehensible. However, for walls and deep beams a stringer-panel model is more convenient because it is less complicated and does not depend on the load case.
Stress in the concrete between the cracks contributes to the stiffness of the reinforcement. This phenomena is commonly referred to as tension-stiffening. In case of tension the effective concrete area is simply defined as the stringer area that results in the correct tension-stiffening.
The first development versions of the graphical user-interface had the name SPMCAD. This name was changed into SPanCAD because the old name turned out to be difficult to remember.
In August 1997 it was announced that Visio will extend its CAD program to support almost all AutoCAD features including AutoLISP [CA-Techniek 1997]. This will introduce competition and prices for AutoCAD licences are expected to drop considerably.
It is common in the finite element method to define the shape of elements with references to nodes. From an information point of view this is efficient since the nodal co-ordinates are only stored once. However, it is also very inflexible. For example, if the position of a node is changed, all elements have to be updated instead of only the ones that are connected to the changed node. An improvement was the development of topological models in which cross links are present not only from an element to its nodes but also from a node to its adjacent elements. In a graphical user-interface the concept of defining element shapes by nodes is even more impractical since it requires that first the nodes are drawn before the element can be inserted. Moreover, it is difficult to explain to a user why an element cannot exist when one of its nodes is deleted. Therefore in SPanCAD a different concept is used: The shape of the stringers and panels is defined by grips independently of the nodes of the model. The components can be moved, reshaped and copied without any reference to nodes. SPanCAD automatically connects the grips of adjacent components by nodes when they occur in a certain radius.
Next to the strut-and-tie method and the finite element method, optimisation methods are being developed that determine the least amount of reinforcement that is required based on plasticity theory (see Section 1.5).
It is common to use the word analysis or stress analysis for the phase of the design in which linear-elastic stresses are computed. If a nonlinear model is used it is commonly referred to as a nonlinear analysis. However, since the nonlinear computation in step 7 has very little to do with stresses, we will use the word simulation instead.
It is not always possible to draw an envelope of physical quantities. For example a largest stress tensor is not defined. Sometimes it is possible to define an envelope but when plotted, it cannot be interpreted properly. For example, if we plot the largest displacements of each point of a three dimensional model for all load combinations, we get a strange shape with holes and overlaps, which by no means improves our understanding of its structural behaviour. The linear stringer-panel model has only shear forces in the panels for which an envelope can be computed. In the nonlinear model, however, an envelope of the panel forces does not exist because it includes not only shear forces but normal forces as well. In this case we can determine the reinforcement in a panel for each load combination and use the largest requirement in each direction. In theory it is even possible to optimise the local reinforcement requirement including all load combinations. Fortunately, often it is sufficient just to choose a convenient minimum reinforcement in the panels.
If parts of a load case can occur somewhat
independently, it is better to split this case into two or more cases.
For example, the dead load of the left-hand span of a bridge can coincidentally
be more that that of the right-hand span. So, it is better to make a separate
load case of the dead load of each span.
The difference between load and strength is not always clear. For example tension in columns due to wind
load can be reduced by the weight of the building. So, structural weight
can contribute to the strength of the structure. Another example is that
during an earthquake we want the structure to absorb much energy, which
will only happen if some ductile parts yield considerably. If these parts
are too strong the whole structure can fail in a brittle manner. So, local
strength can act as a load on the structure.
A stiffness matrix is computed from the model and a load combination. All load combinations will result in the same linear-elastic stiffness matrix if the described displacements have the same direction in each load case. This restriction is adopted in both the linear and the nonlinear stringer-panel model implemented in SPanCAD. Thus, the direction of a described nodal displacement is fixed for a model but its magnitude can vary for each load case. The considerable advantage of identical stiffness matrices is that this matrix needs to be decomposed only once instead of a decomposition for each load combination. Since decomposing the stiffness matrix is the second most time consuming part of a computation, linear processing of multiple load combinations takes little more time than that of only one. Often, described displacements are just zero, however, especially for walls and continuous deep beams, failing supports or irregular settlements can be dominating load cases and should be included in the analysis.
Of course, European codes have similar requirements but these are formulated less conveniently.
The required reliability of a limit state can be determined in several ways. For example, calibration with current codes, monetary optimisation or as a political decision. Often a combination of these methods is used.
Many of the small countries in Europe support a specified reliability in the national codes of practice while the larger countries are yet more reluctant to allow probabilistic computations in design.
This observation as to using average instead of save stiffnesses in computations has been made on several occasions by Eibl. [For example see Eibl 1995].